地球は丸かった Jan. 29, 2018
今日もAGECアウトドアにアクセスいただきありがとうございます。サイト管理人の友人Sです。今回は技術検証です。
コンパスにあまり馴染みのない方はまずこちらの記事を読むことを勧めます。
シルコンの最も大きな特徴は方位角計測機能です。それを利用して地図とコンパスだけで現在地を特定するクロスベアリングっていうテクニックがあります。でもどうしても計測誤差が生じます。
なので、現在地を特定するには理論上は2目標の方位角測定だけでできるのですが、正確性を重視する場合は3か所以上の測定が推奨されるのです。今回はコンパスの種類によってどれだけ誤差が生じて結果にどう影響するのか検証してみましょう。
目次
クロスベアリングとは
一応軽く説明しますけど知ってる人はすっ飛ばして結構です。
①目標物を探します。目視できて、かつ地図上での位置がわかる地物を選びます。
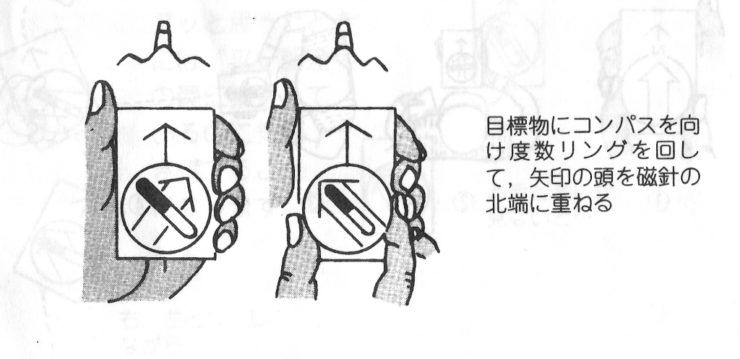
②シルコンのベースプレートの矢印を目標物に向けます。

③度数リングを回してカプセルの矢印を針にあわせます。
シルバコンパス取扱説明書
④地図上の磁北線とカプセルの矢印(又はその平行線)を重ねあわせます。(この時、針は無視)

⑤ベースプレートの縁を使って目標物を通るように線を引きます。
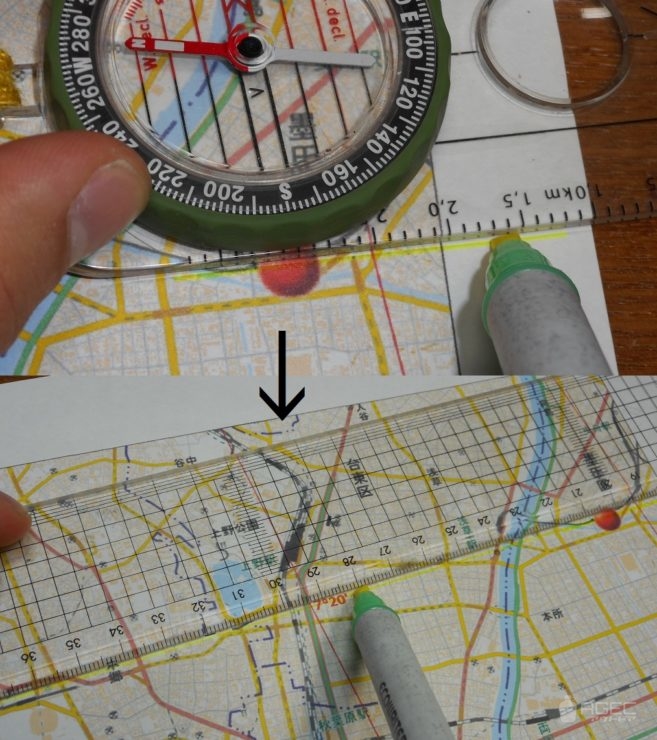
⑥ほかの目標物で①~⑤を繰り返します。線の交点が現在地です。
実験方法
今日は地上105mにある文京シビックセンターの展望台にやって来ました。筆者の個人的な事情でシビックセンターのアクセスが良かっただけなんですけどあそこ無料で穴場的な展望スポットなので結構オススメです。
ここから3種類のシルコンで3方向の目標物の方位角計測をしてみます。って思いきや磁気乱れすぎ!コンパスの針がフラフラ不安定でまったく計測できませんでした。そりゃあ鉄骨の塊なんだから当たり前ですよね。バカだった。。。
というわけで後日3か月後(遅くなってすいません!)、雪も消えた金峰山へ。一般登山道ではなく、チョキ経由で八幡尾根を上がったのでシャクナゲジャングルの突破に苦労しました苦笑。

計測結果と国土地理院の高精度計算サイトで出した数値をもとにQGISっていう専門ソフトで作図して検証してみましょう。
測地系はJGD2000を使います。
基本情報と理論値
偏角
コンパスは真北ではなく、磁北を指します。このズレを偏角と言います。国土地理院の高精度計算サイトで計算した金峰山山頂における偏角の大きさです。
西偏6 °56 ′(=6.93°) source:http://vldb.gsi.go.jp/sokuchi/geomag/menu_04/index.html
使用するコンパス
・普通のシルコン:シルバ レンジャーno3(針精度不明) ・ミラーコンパス:スント MC-2 G(針精度2°) ・レンザティックコンパス:シルバ タイプ54(針精度0.5°)
地物位置情報(JGD2000)
目標地点として、富士山、北岳、瑞牆山を選びました。座標値は国土地理院のサイト記載のものです。
計測基点:金峰山(N35°52′17″, E138°37′31″) 目標点①:富士山(N35°21′39″, E138°43′39″) 目標点②:北岳(N35°40′28″, E138°14′20″) 目標点③:瑞牆山(N35°53′36″, E138°35′31″) source:http://www.gsi.go.jp/KOKUJYOHO/MOUNTAIN/mountain.html
方位角の計算値
計測基点(金峰山山頂)から見たときの各目標地点の方位角の理論値です。国土地理院の高精度計算サイトで計算したものです。(今回使用する測地系はJGD2000なので楕円体はGRS80を選択して計算)
目標点①:170°41′06.37″ (≒170.6851028°) 目標点②:238°05′20.64″ (≒238.0890667°) 目標点③:308°58′51.89″ (≒308.9810806°) source:https://vldb.gsi.go.jp/sokuchi/surveycalc/surveycalc/bl2stf.html
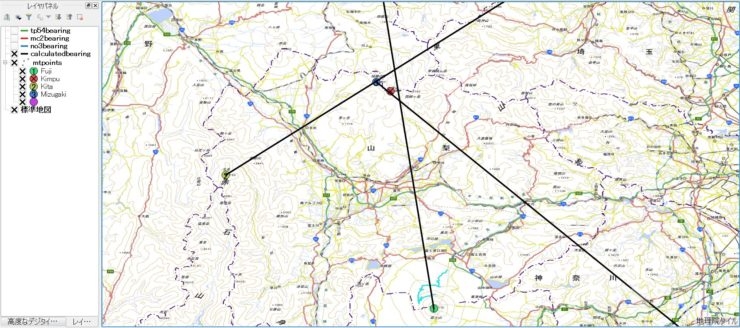
一点に定まらない理由
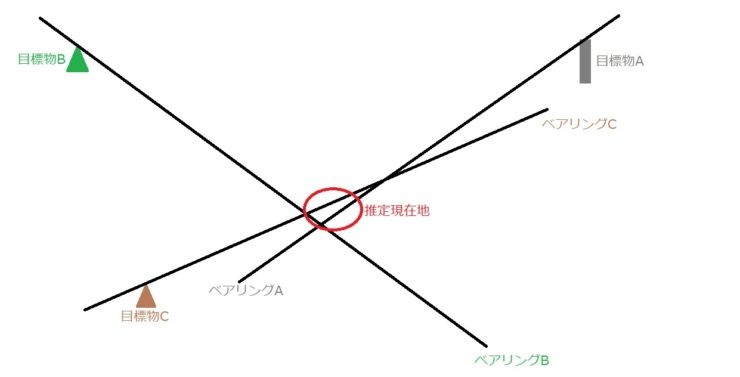
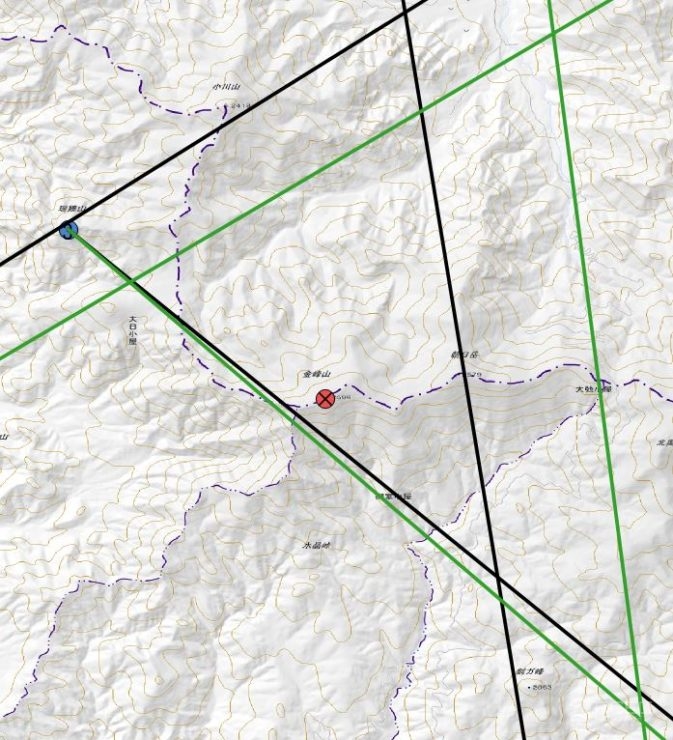
さて、計算値の角度ですが、実際に作図してみると一点で交わらずに推定現在地が結構大きい範囲になっています↓。
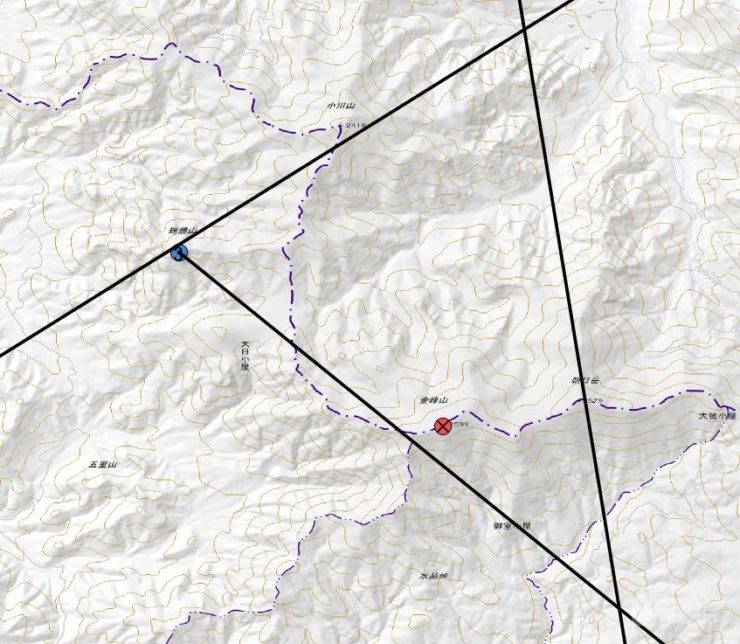
なぜでしょうか?
まず、考えられる理由の一つ目は理論値は計算の結果でしかないので現実の角度とは一致しないこと。これは正しいでしょう。でも理由はこれだけではありません。
もう一つの理由は、
現実世界での直線は(ほとんどの)地図上では曲線
だからです。これは地球が平面ではなく、実際には楕円体(に近い立体)だからです。よくわからない人は等角航路と大圏航路の違いをググってみて下さい。
厳密な話をすれば、
計測基点→目標物 の方位角と
目標物→計測基点 の方位角は違うので、
長距離の目標物は作図時に注意が必要です。
今回は直線を作図するのにQGISの“Azimuth and Distance Plugin”というものを使いましたが、CAD的な性格が強くて、現実世界で真っすぐであることではなく、真北に対する角度を一定にする意味で真っすぐな線を引いています。なので今回は国土地理院の計算値を基準に考えることにします。
以下の画像を見る時は三角形の大きさではなく、黒線(計算値)からのズレに注目してください。
結果
※数値について
計測値:実際にコンパスで測定された数値。磁北を基準とした方位角。
偏角補正値:計測値から偏角分のズレを差し引いたもの。真北を基準とした方位角。
誤差:偏角補正値と計算で得られた理論値の間のズレ。
誤差平均:誤差の平均値。コンパスの針精度と測定精度が影響。
誤差標準偏差:誤差の標準偏差。コンパスの測定精度が影響。
普通のシルコン
シルコンを覗き込みながらそれっぽく角度を測ります。それでも測ってみると結構精度は高めなのでハイキング程度なら問題ありません。はっきり言って普通の人にはこの手の一般的なシルコンがベストです。
No.3 | 計測値 | 偏角補正値 | 誤差 |
| 目標物① | 181° | 174.07° | +3.38° |
| 目標物② | 247° | 240.07° | +1.98° |
| 目標物③ | 315° | 308.07° | -0.91° |
誤差の平均:1.4833°
誤差の標準偏差:1.78625°
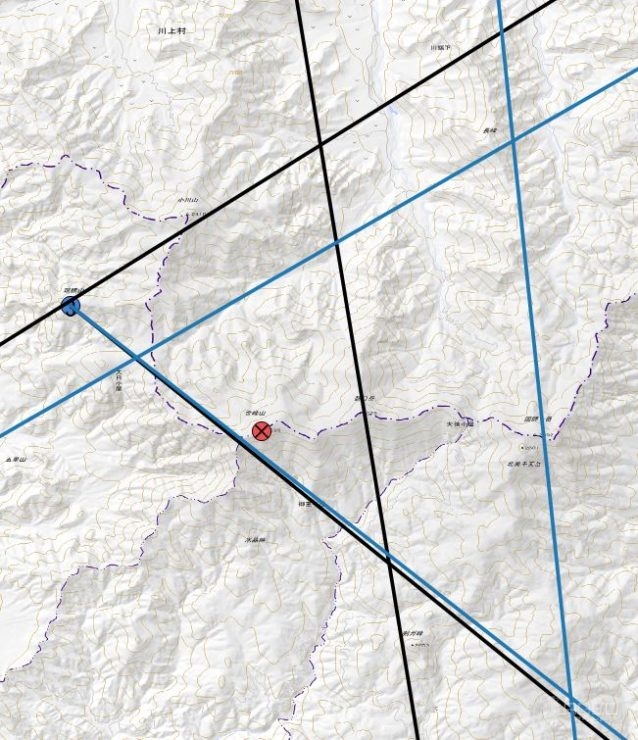
ミラーコンパス
ミラーにカプセルを映し出せるのでより高精度で方位角計測できます。ミラーの基準線と目標物と針の軸を一直線上に維持しながら度数リングを回すってのが結構めんどくさいのですが、普通のシルコンよりもかなり高精度で計測できます。
| MC-2G | 計測値 | 偏角補正値 | 誤差 |
| 目標物① | 176° | 169.07° | -1.62° |
| 目標物② | 244° | 237.07° | -1.02° |
| 目標物③ | 314° | 307.07° | -1.91° |
誤差の平均:ー1.5167°
誤差の標準偏差:0.370615°
レンザティックコンパス
さすが測量用。先ほどの2つは度数リングを回してコンパスの針とカプセルの矢印を合わせなければならないのでめんどいのですが、こいつの場合はレンズを覗き込むだけなので楽です。
| type54 | 計測値 | 偏角補正値 | 誤差 |
| 目標物① | 179.5° | 172.57° | +1.88° |
| 目標物② | 246.5° | 239.57° | +1.48° |
| 目標物③ | 317.5° | 310.57° | +1.59° |
誤差の平均:1.65°
誤差の標準偏差:0.168721°
3つの比較
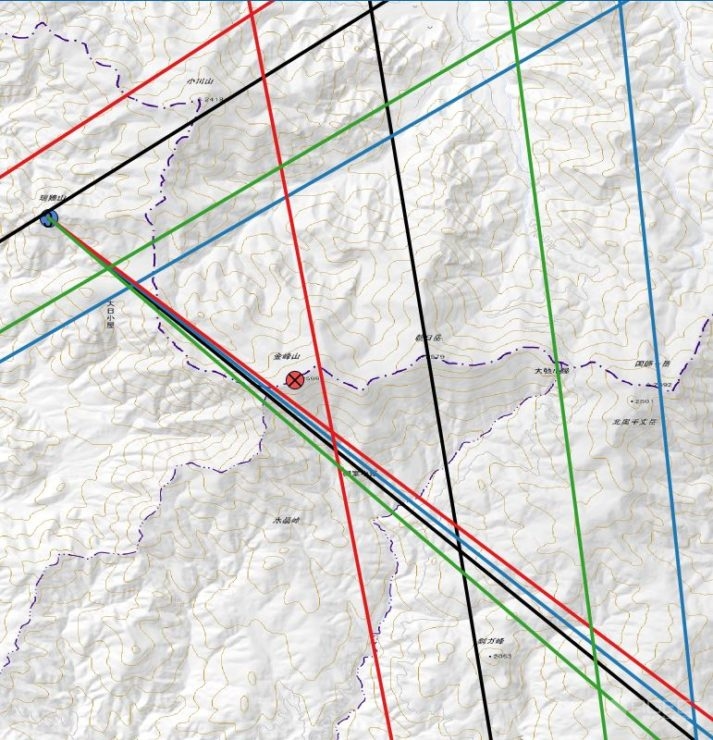
誤差の平均を比べるとシルバはどちらも+1.5°くらいで、もしかしてシルバの針製造過程で磁性を与える時の基準が僅かに東にズレているのかもしれません。サンプル数が少なすぎてはっきりしたことは何ともいえませんが。
考察
誤差には2つの要素があります。
①針精度
②測定精度
①針精度はコンパスの針が実際に指す向きが磁北からどれくらいズレているかです。精度の面におけるコンパスの針の性能です。ひとつひとつのコンパスがその個体固有の値を取ります。
②測定精度は方位角の実際の測定行為における読み取り精度です。サイティングコンパスはこの測定精度を改善するために開発されたものです。測定精度はコンパスの種類のみならず、気象的要因、地形的要因、測定者の視力などが影響を及ぼします。
さて、これらの誤差はどう数値化されるか。コンパスで実際に方位角測定をして計算値との誤差を求める、という行為を何回も何回も繰り返していけば、誤差のサンプルがたくさん集まります。誤差のサンプルが増えるにつれて段々と、
・誤差の平均は①針精度に近づいていきます
・誤差の標準偏差は②測定精度に近づいていきます
今回は3目標しか測定していないので誤差の平均はあんまりあてにならないと思いますが、標準偏差を見てみると驚くことにコンパスによって大きな差がみられます。タイプ54ではたったの0.17°しかありません。
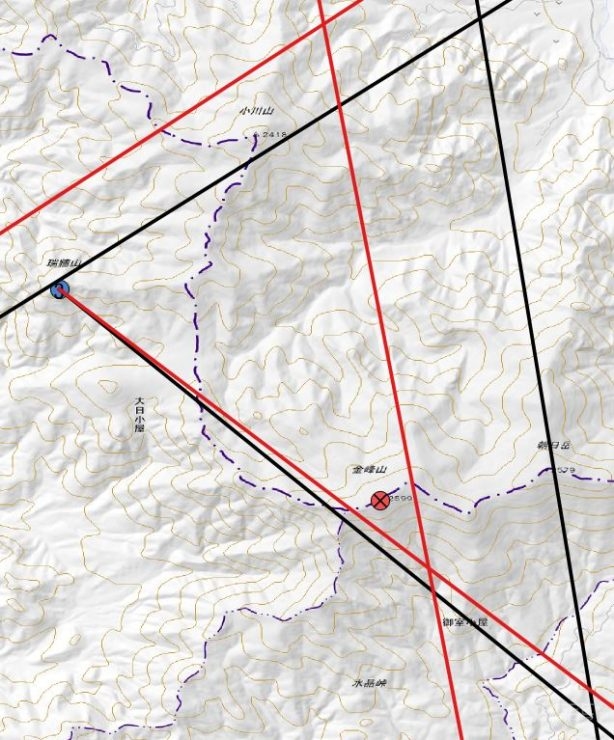
シルバコンパスを用いた計測で重要になるのは①針精度です。これは測定という行為に関係なく不変的に一定の角度でズレているからです。偏角を補正するときに針がどれくらい磁北からズレているか知っておくと精度が全然違うと思います。特にサイティングコンパスでは誤差標準偏差、即ち②測定精度がかなり小さいので誤差はほとんど①針精度で決まります。タイプ54を誤差平均1.65°で補正したらこうなります↓。驚くほど高精度です。
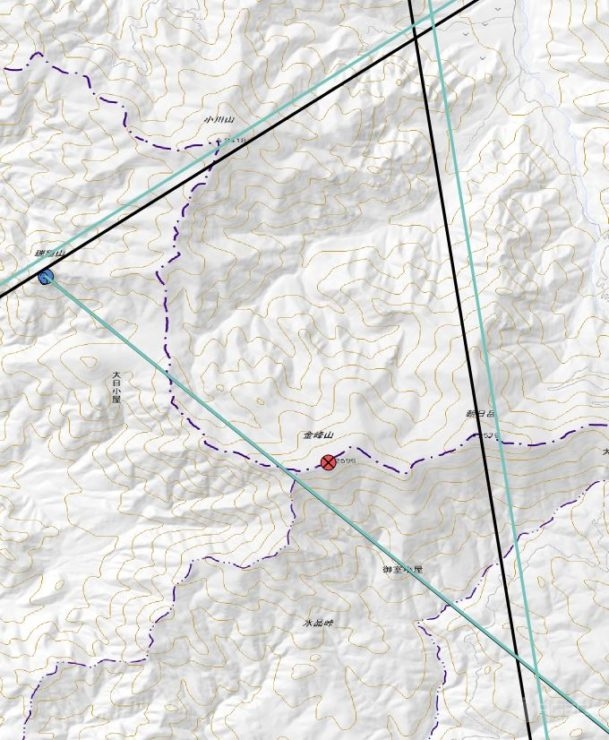
参考までに、誤差標準偏差の小さいtype54で測った3点のデータからt分布を利用して信頼係数95%で平均を推定してみました↓。
x-tα/2(n-1)σ/√n≦μ≦x+tα/2(n-1)σ/√n 1.65-t0.025(2)0.168721/√3≦μ≦1.65+t0.025(2)0.168721/√3 1.65-0.41916≦μ≦1.65+0.41916 1.23≦μ≦2.07
まとめ
日本国内でクロスベアリングを使う場面はまず無いでしょう。現在地推定において、隣の稜線のピークが何度くらいの方向にある、などといった情報を補完的につかうことはあっても日本の入り組んだ地形を読み解くのが基本です。
クロスベアリングを行う場合にも注意点がいくつかあります。
・コンパスの針には誤差がある
・コンパスの方位角の読み取り精度には限界がある
・気象の影響を受ける上、人間の視力には限界がある
・現実世界の直線は地図上では直線ではない
これらの要因をコントロールできない場合は誤差が非常に大きくなります。高精度な計測をするためにはサイティングコンパスを使用することは効果的です。しかし、コンパスの種類をこだわるだけではダメです。あらかじめ使用するコンパスの針精度を知っておいて、作図時に偏角と針の誤差の両方を補正しておくことの方が精度を向上するうえで重要です。
結論として、肉眼でくっきりと目標物が視認できる限られた狭い範囲内でのみクロスベアリングは有効に使えます。
国土地理院コンテンツ利用規約に基づく表記
本記事の地形図を含んだ画像は国土地理院が提供する地理院タイルをJGD2000で表示したものです。